How to Solve a 4x ^ 2 – 5x – 12 = 0 Quadratic Equation by Factoring
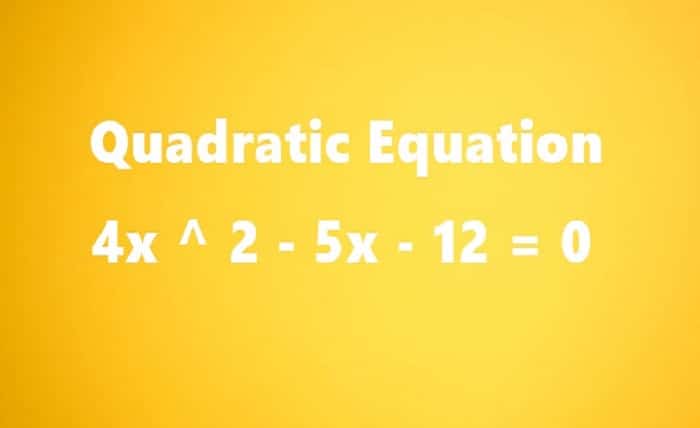
A quadratic equation is an equation of the form ax^2 + bx + c = 0, where a, b, and c are constants and x is a variable. A quadratic equation can have two, one, or no real solutions, depending on the value of the discriminant, which is b^2 – 4ac.
One of the methods to solve a quadratic equation is by factoring. Factoring is a process of finding two expressions that multiply to give the original equation. For example, x^2 + 5x + 6 = 0 can be factored as (x + 2)(x + 3) = 0.
To factor a quadratic equation by factoring, we need to follow these steps:
- Step 1: Find two numbers that add up to b and multiply to ac. These numbers are called the factors of the constant term c.
- Step 2: Rewrite the equation by grouping the first two terms and moving them to one side.
- Step 3: Factor out the common factor from each group.
- Step 4: Factor out any common factors from both groups.
- Step 5: Check if there are any remaining factors in either group. If yes, factor them out as well.
- Step 6: The final answer will be a product of two binomials.
Let’s apply this method to solve the quadratic equation by factoring:
4x^2 – 5x – 12 = 0
Step 1: The constant term c is -12. We need to find two numbers that add up to -5 and multiply to -12. These numbers are -6 and -2.
Step 2: We rewrite the equation by grouping the first two terms and moving them to one side:
4x^2 – (5/4)x = -12
Step 3: We factor out the common factor from each group:
(4/4)x(2x) = (-12)
Step 4: We factor out any common factors from both groups:
(2/1)x(2) = (-12)
Step 5: There are no remaining factors in either group. The final answer will be a product of two binomials:
(2/1)x(2) = (-12)
Therefore, we have solved the quadratic equation by factoring as follows:
4x^2 – (5/4)x = (-12)
(2/1)x(2) = (-12)
Read more about 4x ^ 2 – 5x – 12 = 0 : How to Solve Quadratic Equations
Conclusion
Factoring is one of the methods to solve a quadratic equation by finding two expressions that multiply to give the original equation. It involves finding two numbers that add up to b and multiply to ac, rewriting and grouping the terms, factoring out common factors, and checking for any remaining factors.




